Global Scientific Research in Environmental Science

To unify gravitational interaction with other three kinds of interaction are a work hadn’t been finished by Albert Einstein and a big problem that human must solve to continue living in the universe. As the covariant derivative in gravitational theory, i.e., ∇_μψ^λ=∇_μψ^λ+Γ_μν^λψ^λ in general relativity has similar structure to that ∇_μψ_λ=∂_μψ_λΓ_μλ^νψ_λ in gauge theory, D_μψ_i=∂_μψ_i-ieq_iA_μψ_i(it is worth mentioning that  for the covariant derivative for a covariant vector), people asked whether there would some links between the connection Γ_μν^λ (or Γ_μλ^ν for covariant vector) and the graviton, and whether gravity could be described by a gauge theory. Starting from quantum mechanics, the relationship between symmetry and the invariance of the Lagrangian may be the essence of the gauge invariance e^{(iq_i θ)}D_μψ_i=D_μe^(iq_iθ)ψ_i in gauge theory, which represents the invariance of Lagrangian under a gauge transformation; therefore, a gauge theory of gravity may also be built in a similar way from this relationship by 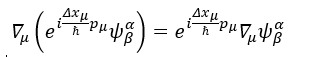for which reason the covariant derivative of a tensor ∇_μψ_β^α must remain to be a tensor as the original tensor ψ_β^α, and it leads to the existence of connection  Γ_μν^λ or Γ_μλ^ν .

The conservation law has theoretical explanation in quantum mechanics. When there is a symmetry, the system, i.e., a state would keep invariant after a transformation which is under this symmetry.

Supposing there is a symmetry A, the transformation under this symmetry is  an arbitrary state is ψ, then ψ would be invariant under transformation Â, that is,

Einstein’s gravitational ^1-3

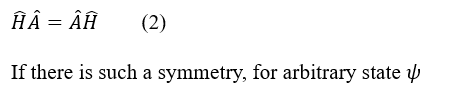
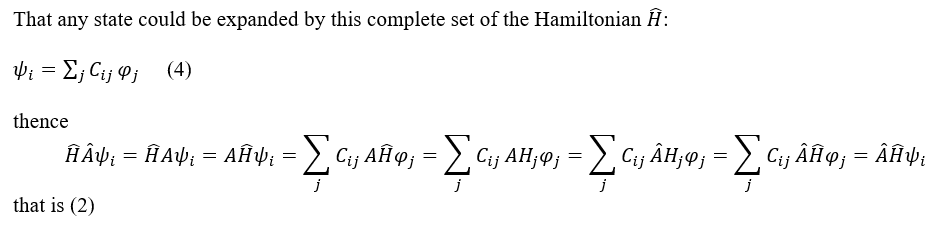
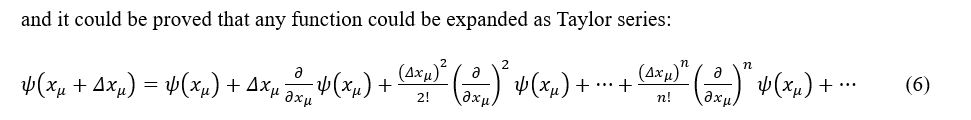
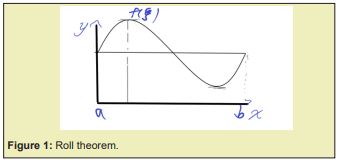
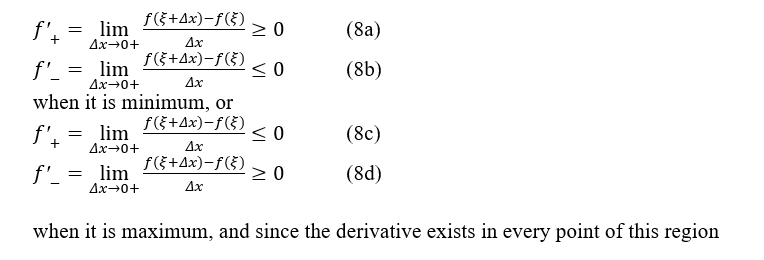
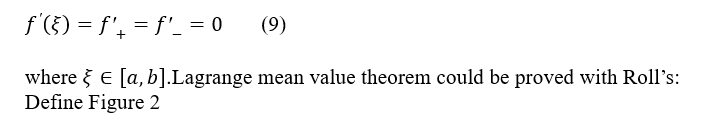
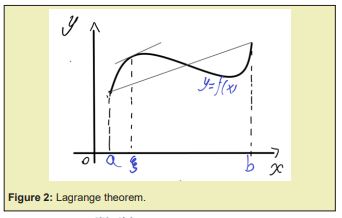
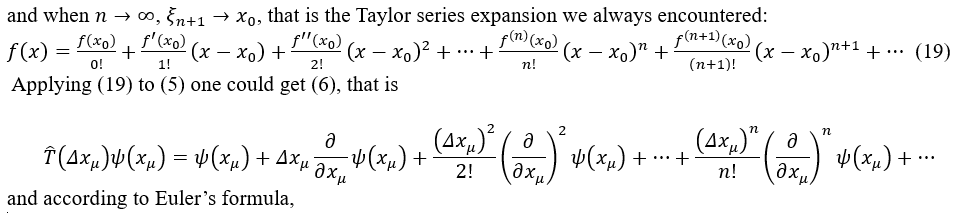
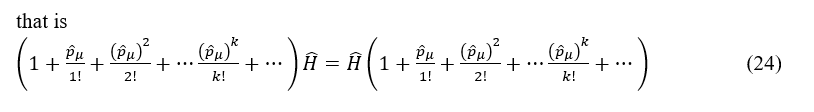
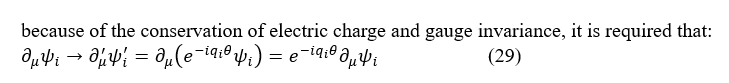
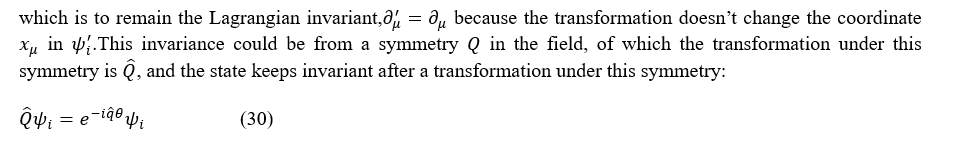
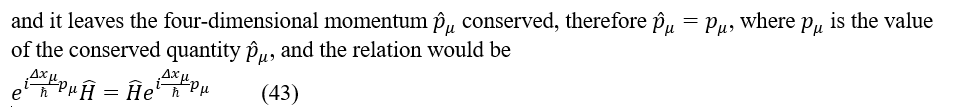
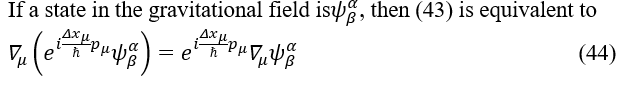
Thanks to everyone.

None.

Author declares that there is no conflict of interest.

1. 1. Qian Bochu. Quantum Mechanics. Higher Education Press. Beijing.
2. 2. Duan Yishi. General relativity and gravitational gauge theory. Science Press. Beijing.
3. 3. Yang CN. Gauge invariance in classical field theories. Phy Rep. 1978;9C:1.